To give perspective to the New Theory of Flight presented on this site, let us see how the Old Theory of Flight is presented in the classical text Fundamentals of Aerodynamics by John D. Anderson. We quote from and comment on the essential Chapter 4 Incompressible Flow Over Airfoils:
2d Flow around Airfoil Sections
- In the period 1912-1918, the analysis of airplane wings took a giant step forward when Ludwig Prandtland his colleagues at Gottingen, Germany, showed that the aerodynamic considerationof wings could be split into two parts: (1) the study of the section of a wing-an airfoil-and (2) the modification of such airfoil properties to account for the complete, finite wing.
- This approach is still used today; indeed, the theoretical calculation and experimental measurement of modern airfoil properties have been a major part of the aeronautics research carried out by the National Aeronautics and Space Administration (NASA) in the 1970s and 1980s.
Anderson here presents the basic assumption of the Old Theory: 2d flow around an airfoil section can be used as a meaningful simplification of real flow around a real 3d airfoil.
We show in our work that this is not the case since the real flow is 3d with in particular a completely crucial 3d separation pattern which cannot be captured by restriction to 2d. This is the fundamental error of The Old Theory which has led to the invention of a circulation theory of flight without connection to reality and thus without real predictive value. The New Theory on the other hand offers a wealth of predictions and thus measured against Popper’s falsifiability criterion is a scientific theory, while the Old Theory is not.
Introduction of Vortex Sheet
- The concept of replacing the airfoil surface in Fig. 4.10 with a vortex sheet is more than just a mathematical device; it also has physical significance. In real life, there is a thin boundary layer on the surface, due to the action of friction between the surface and the airflow (see Fig. 1.28).
- This boundary layer is a highly viscous region in which the large velocity gradients produce substantial vorticity; i.e., V’ xV is finite within the boundary layer. (Review Sec. 2.12 for a discussion of vorticity.) Hence, in real life, there is a distribution of vorticity along the airfoil surface due to viscous effects, and our philosophy of replacingthe airfoil surface with a vortex sheet (such as in Fig. 4.10) can be construed as a way of modeling this effect in an inviscid flow.
We here see the effect of a no-slip boundary layer generating transversal vorticity distributed around the wing section. Here is a typical picture of cross-section of a vortex sheet with transversal vorticity distributed around the wing surface supposed generated by friction in a boundary layer:
The Kutta Condition
- Reflecting on Figs. 4.12 and 4.13, we emphasize again that in establishing the steady flow over a given airfoil at a given angle of attack, nature adopts that particular value of circulation (f2 in Fig. 4.12) which results in the flow leaving smoothly at the trailing edge. This observation was first made and used in a theoretical analysis by the German mathematician M. Wilhelm Kutta in 1902. Therefore, it has become known as the Kutta condition.
Here the Kutta condition is introduced as a condition which Nature for some reason would seek to satisfy.
The Mechanism: Starting Vortex
- This brings us to the summary as well as the crux of this section. As the flow over an airfoil is started, the large velocity gradients at the sharp trailing edge result in the formation of a region of intense vorticity which rolls up downstream of the trailing edge, forming the starting vortex. This starting vortex has associated with it a counterclockwise circulation. Therefore, as an equal-and opposite reaction, a clockwise circulation around the airfoil is generated. As the starting process continues, vorticity from the trailing edge is constantly fed into the starting vortex, making it stronger with a consequent larger counterclockwisecirculation. In turn, the clockwise circulation around the airfoil becomes stronger,making the flow at the trailing edge more closely approach the Kutta condition, thus weakening the vorticity shed from the trailing edge. Finally, the starting vortex builds up to just the right strength such that the equal-and-oppositeclockwise circulation around the airfoil leads to smooth flow from the trailing edge (the Kutta condition is exactly satisfied). When this happens, the vorticity shed from the leading edge becomes zero, the starting vortex no longer grows instrength, and a steady circulation exists around the airfoil.
Here large scale circulation is explained as Nature’s way of satisfying Kelvin’s theorem dictate of zero total vorticity.
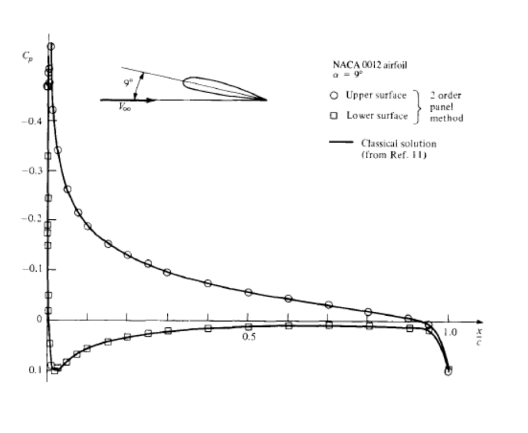
Non-Physical Pressure Distribution
In the picture below we see the pressure distribution on the upper and owed surface of a wing section at an angle of attack of 9 degrees. We see high pressure at the trailing edge which is not observed in real flow: The KZ solution has zero drag and is therefore non-physical.
4.5.1 Without Friction Could We Have Lift?
- We noted that lift on an airfoil is primarily due to the surface pressure distribution…. Hence pressure is the dominant player in the generation of lift, and shear stress has a negligible effect on lift. It is for this reason that the lift of an airfoil below stall can be accurately predicted by inviscid theories…
- Howevr, if we lived in a perfectly inviscid world, an airfoil could not produce lift. Indeed, the presence of friction is the very reason why we have lift. These sound like strange, even contradictory statements. What is going on here? The anwer is that in real life, the way that nature insures that the flow will leave smoothy at the trailing edge….is that the viscous boundary layer remains attached to the surface all the way to the trailing edge. Nature enforces the Kutta condition by friction. If there were no boundary layer (i.e. no friction), there would be no physical mechanism in the real world to achieve the Kutta condition.
We see here the contradictory logic of the Kutta-Zhukovsky circulation theory of lift: Viscosity is both inessential and completely essential. Anderson’s question What is going on here? is fully adequate and clearly expresses the non-physical character of 2d circulation theory of lift.
(Notice that Section 4.5.1 is added in the 2001 edition of the book, apparently in an effort to meet an obvious and pertinent question).
Unsuccessful Interview with John D. Anderson
Under Interviews you find an unsuccessful attempt of mine to ask John D some perfecty innocent questions connecting to his statement in Introduction to Flight:
- As Curator of Aerodynamics at the Smithonian’s National Air Space Museum the author is frequently asked by visitors how a wing produces lift – a natural and perfectly innocent question. Unfortunately there is no satisfactory one-liner for an answer. Even a single paragraph does not suffice. After a hundred years since the Wright Flyer, different people take different points of view about what is the most fundamental mechanism that produces lift, some pressing their views with almost religious fervor.